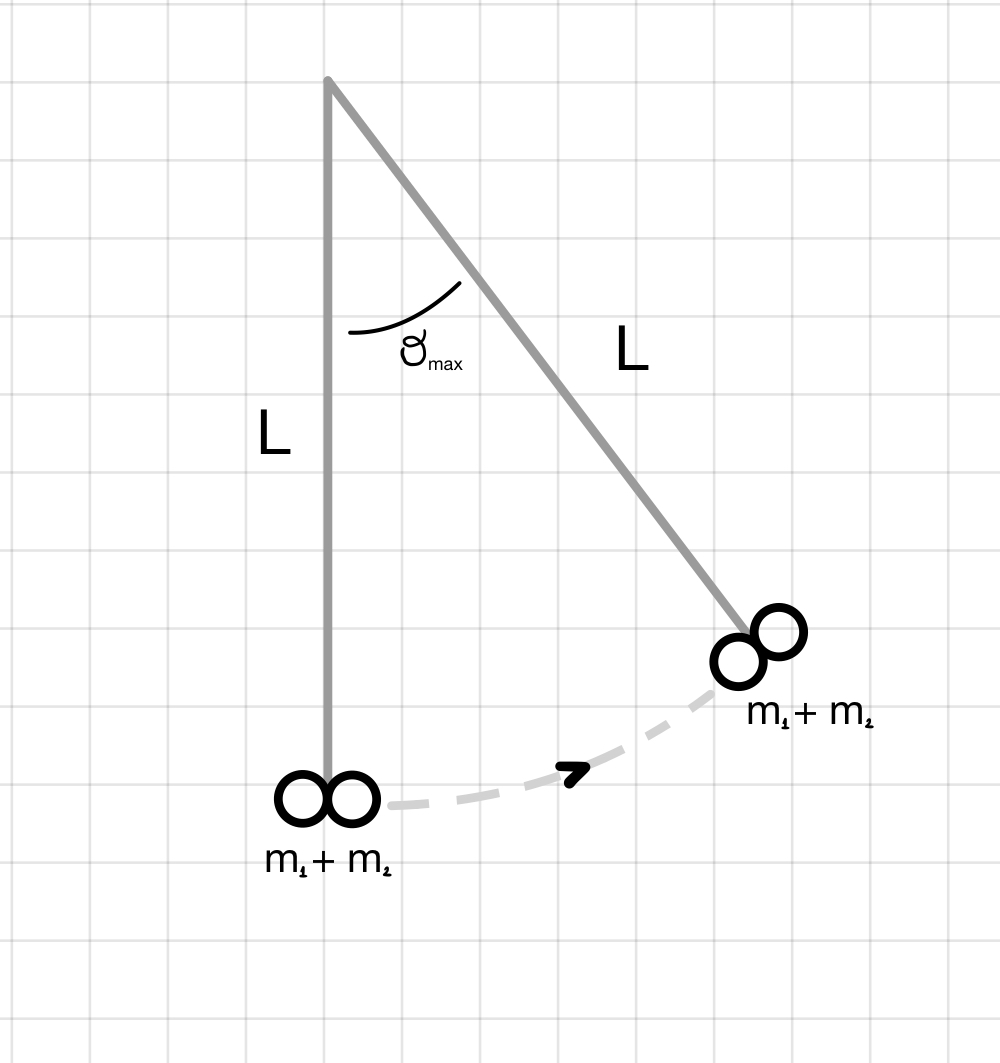
Due sfere di massa $m_1 =m_2$ sono appese allo stesso perno $O$ tramite due fili di uguale lunghezza $L$.
Se $m_1$ viene portata fuori dalla verticale di una quantità $h$ e lasciata andare urta $m_2$. Determinare l'equazione del moto del sistema, se:
$Richieste$
$1)$ L'urto è completamente anaelastico
$2)$ L'urto è perfettamente elastico
$3)$ Descrivere il tipo di moto se l'urto è perfettamente elastico ma si tiene conto della resistenza (viscosa)
dell'aria
$Risposte:$
$1)$ Nel caso di un urto completamente anaelastico le due particelle procedono unite, come un unico pendolo di massa $m_1+m_2$.
il periodo $T$ di tale pendolo non dipende dalla massa ed è pari a:
$T=2\pi\sqrt{\frac{L}{g}}$
L'ampiezza del moto si ottiene calcolando la velocità immediatamente dopo l'urto, applicando la conservazione della quantità di moto:
$m_1 *v_1 = (m_1+m_2)*v$
dove $v_1$ è la velocità della massa $m_1$ e $v$ è la velocità dopo l'urto
dove $v^2=2gh$ --> $v= \sqrt{2gh}$ $g$ è l'accelerazione di gravità e h altezza della massa $m_1$
$v_1=\frac{m_1}{m_1+m_2}*v = \frac{m_1}{m_1+m_2}* \sqrt{2gh} =$
dal testo del problema sappiamo che $m_1 =m_2$ quindi
$= \frac{m_1}{m_1+m_2}* \sqrt{2gh} = \frac{m_1}{2m_1}* \sqrt{2gh} = \frac{\sqrt{2gh}}{2}$
applicando la conservazione dell'energia meccanica al pendolo di massa $m_1+m_2$ avremo che la quota massima $h_{max}$ sarà data:
$h_{max} = \frac{v}{2g} = \frac{2gh}{4}*\frac{1}{2g} = \frac{h}{4}$
Ora abbiamo trovato tutto il necessario per determinare dell'equazione del moto!
L'angolo di oscillazione massimo $\theta_{max}$ sarà dato da:
$\theta_{max} = arccos(\frac{L-h_{max}}{L}) = arccos(1-\frac{h}{4L})$
l'equazione del moto sarà dunque:
$\theta = \theta_{max}*sin(\omega t)$
con $\omega = 2\pi * \frac{L}{g}$ e $\theta_{max} =arccos\left(1-\frac{h}{4L}\right)$
$2)$ Nel caso di un moto perfettamente elastico:
dopo l'urto la massa $m_1$ resta ferma e la seconda ($m_2$) procede con velocità:
$v= \sqrt{2gh}$ cioè con la stessa velocità che aveva la massa $m_1$ prima dell'urto
Le due masse si muovono come un pendolo semplice di massa $m$ e periodo $T=2*\pi*\sqrt{\frac{L}{g}}$ alternativamente con ampiezza massima:
$\theta_{max}=arccos\left(\frac{L-h}{L}\right) =arccos\left(1-\frac{h}{L}\right)$
$3)$ Nel caso tenessimo conto dell'attrito viscoso dell'aria con l'urto che è perfettamente elastico:
le due masse si muoverebbero alternativamente come nel caso $2)$ ma l'ampiezza delle oscillazioni diminuirà gradualmente. Lo pseudoperiodo sarà sempre:
$T=2\pi\sqrt{\frac{L}{g}}$